Calcular la altura que tendría la atmósfera si no
variase la densidad del aire con la altura:
1. 8 km.
2. 722 km.
3. 10518 m.
4. 10336 m.
5. 722 m.
¿Cómo lo haríais? La respuesta correcta seria la primera.
Gracias!!
Moderador: Alberto
por favor, alguien que sepa ,los calculosdrflecha escribió:es sencillo usá la formula de la presion p=d*g*h aver si alcanzas a resloverlo. tan simplemente despeja la altura con 1amosfera de presion y la densidad deñl aire. ya con eso sale
alguno sabe resolver esta
21.
La ecuación del movimiento de un móvil es r=ti + Ln(t+1)j, donde r se expresa en metros y t en segundos. Si denotamos aT como el vector ace-leración tangencial y aN como el vector acelera-ción normal, en t=3 seg, se cumple:
Datos: “i” y “j” son vectores unitarios.
1. |aT|=1.18|aN|
2. |aT|=0.03|aN|
3. |aT|=0.25|aN|
4. |aT|=0.15|aN|
5. |aT|=0.73|aN|
es del ultimo año porqmas qe lo intento ni modo
por favor, alguien que sepa ,los calculos[/quote]drflecha escribió: alguno sabe resolver esta
21.
La ecuación del movimiento de un móvil es r=ti + Ln(t+1)j, donde r se expresa en metros y t en segundos. Si denotamos aT como el vector ace-leración tangencial y aN como el vector acelera-ción normal, en t=3 seg, se cumple:
Datos: “i” y “j” son vectores unitarios.
1. |aT|=1.18|aN|
2. |aT|=0.03|aN|
3. |aT|=0.25|aN|
4. |aT|=0.15|aN|
5. |aT|=0.73|aN|
es del ultimo año porqmas qe lo intento ni modo
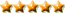
Facilito, facilito. Pero vayamos paso a paso.iflores escribió:por favor, alguien que sepa ,los calculosdrflecha escribió: alguno sabe resolver esta
21.
La ecuación del movimiento de un móvil es r=ti + Ln(t+1)j, donde r se expresa en metros y t en segundos. Si denotamos aT como el vector ace-leración tangencial y aN como el vector acelera-ción normal, en t=3 seg, se cumple:
Datos: “i” y “j” son vectores unitarios.
1. |aT|=1.18|aN|
2. |aT|=0.03|aN|
3. |aT|=0.25|aN|
4. |aT|=0.15|aN|
5. |aT|=0.73|aN|
es del ultimo año porqmas qe lo intento ni modo
Es la definición más general de la aceleración normal. En la fórmula que tú pones, ése 'r' es el radio de curvatura, que se calcula a partir de las derivadas primeras y segundas de la trayectoria (ergo, de la componentes de la velocidad y aceleración). Si miras en la wiki: https://es.wikipedia.org/wiki/Radio_de_curvatura y operas un poco, verás que tu expresión y la mía son completamente equivalentes.Mr_Robinson escribió:
Una pregunta, esa definición de aceleración normal de dónde sale?La has sacado de algún libro? No es más sencillo calcular módulos de \(v\) y de \(r\) y hacer directamente \(a_N=\frac{v^2}{r}\) ??
En el examen dudo que haya tiempo de hacer tanto cálculo la verdad...
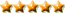
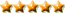
Pues tienes toda la razón, no tiene que ver vector de posición con radio de curvatura, curioso que salga el resultado casi casiiflores escribió:Es la definición más general de la aceleración normal. En la fórmula que tú pones, ése 'r' es el radio de curvatura, que se calcula a partir de las derivadas primeras y segundas de la trayectoria (ergo, de la componentes de la velocidad y aceleración). Si miras en la wiki: https://es.wikipedia.org/wiki/Radio_de_curvatura y operas un poco, verás que tu expresión y la mía son completamente equivalentes.Mr_Robinson escribió:
Una pregunta, esa definición de aceleración normal de dónde sale?La has sacado de algún libro? No es más sencillo calcular módulos de \(v\) y de \(r\) y hacer directamente \(a_N=\frac{v^2}{r}\) ??
En el examen dudo que haya tiempo de hacer tanto cálculo la verdad...
Vaya, que no hay mucho donde rascar. Y sobre el tiempo... En esto se tarda más o menos un minuto. Aquí parece mucho porque lo puse todo muy detalladito para facilitar que se entendiese bien, pero son cuatro calculitos rápidos. O bueno, eso me parece a mí.